Математические хитрости: иррациональные числа в дробной форме с корнем
На этой странице вы найдете полезные советы и методы по преобразованию иррациональных чисел в дробные выражения с корнями. Погрузитесь в мир математики, где сложные концепции становятся простыми и понятными.


Для начала определите, является ли ваше число действительно иррациональным, анализируя его периодичность и представление в десятичной форме.

Как разобраться в корнях ? Квадратный корень 8 класс - Математика TutorOnline

Иррациональные числа часто можно представить как корень из числа. Попробуйте записать ваше число в форме корня, чтобы упростить дальнейшие преобразования.

Рациональные, иррациональные и действительные или вещественные числа. Извлечение корня. Алгебра 8 кл


Используйте метод рационализации знаменателя для упрощения дроби с корнем. Этот метод заключается в умножении числителя и знаменателя на сопряженное выражение.

Разложить иррациональное число в цепную дробь


Преобразуйте выражение в форме корня, если возможно, чтобы получить более удобное численное представление. Это позволит вам использовать дроби для дальнейших вычислений.

1.8 Комплексные числа

Если число выражено как периодическая десятичная дробь, постарайтесь выявить закономерности, которые помогут преобразовать его в обычную дробь.

Иррациональность sqrt2


Пользуйтесь калькулятором для проверки ваших преобразований. Современные калькуляторы могут автоматически выполнять операции с корнями и иррациональными числами.
Запомните основные свойства корней, такие как правило умножения и деления, чтобы быстрее решать задачи с иррациональными числами.

Рациональные и иррациональные числа за 5 минут

Используйте графики для визуализации иррациональных чисел и их дробных форм. Это может облегчить понимание и помочь в решении сложных задач.

Математика для всех. Алексей Савватеев. Лекция 6.6. Иррациональность корня из двух - 2
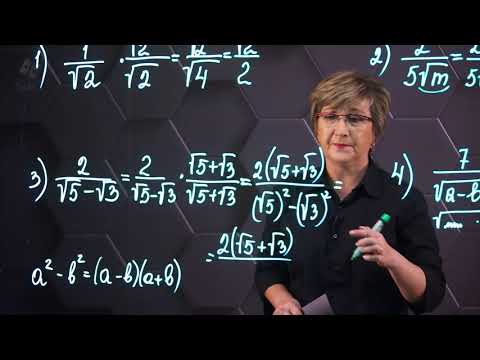
Преобразование выражений, содержащих квадратные корни. Избавление от иррациональности. 8 класс.
Практикуйтесь на простых примерах, чтобы постепенно улучшать свои навыки работы с иррациональными числами в дробных выражениях.

Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнем
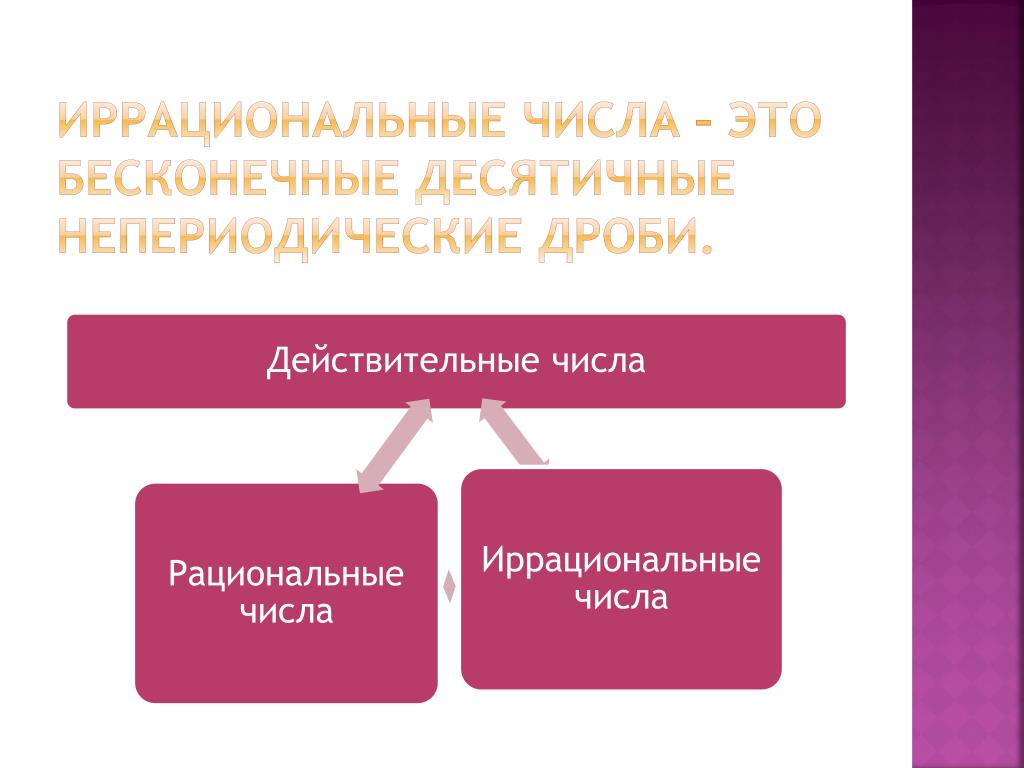
Консультируйтесь с преподавателями или пользуйтесь учебными пособиями, чтобы разобраться с трудными аспектами и углубить свои знания в этой теме.

Алгебра 8. Урок 8 - Квадратный корень. Освобождение от иррациональности

