Преимущества и примеры применения квадратных и диагональных матриц
В этой статье мы рассмотрим основные свойства квадратных и диагональных матриц, их применение в различных областях математики и смежных дисциплин. Вы найдете примеры их использования, а также полезные советы по работе с этими матрицами.

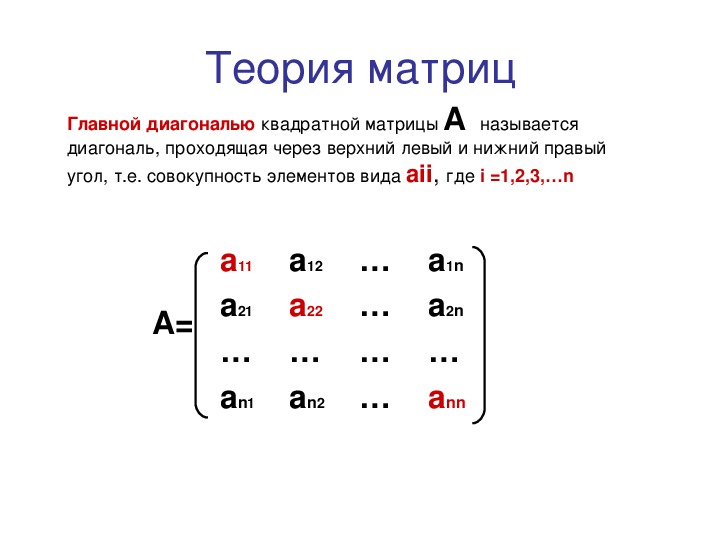

Понимание основных свойств квадратных матриц, таких как определитель и след, поможет вам в решении многих задач линейной алгебры.

Новинка: Arturia PolyBrute 12 — новый уровень в мире синтезаторов. Большой обзор + РОЗЫГРЫШ
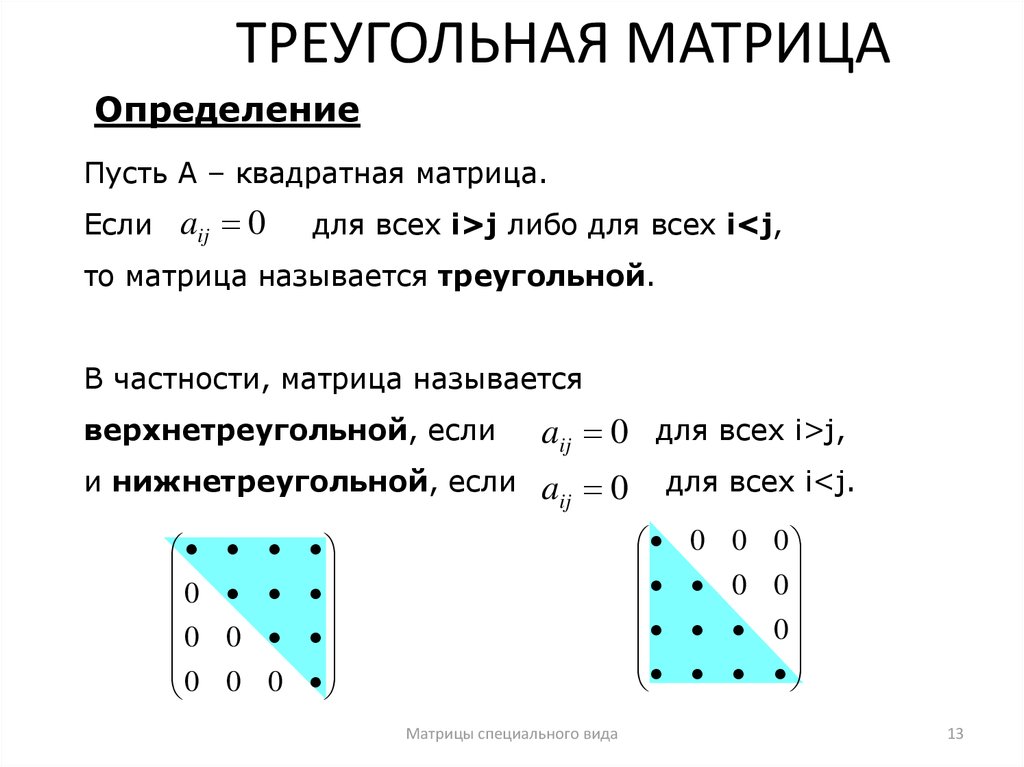

Диагональные матрицы особенно полезны для упрощения вычислений при решении систем линейных уравнений и векторных преобразований.

Диагональная матрица линейного оператора
Используйте диагональные матрицы для ускорения вычислений в алгоритмах машинного обучения и обработки данных.

Сумма элементов матрицы на главной диагонали

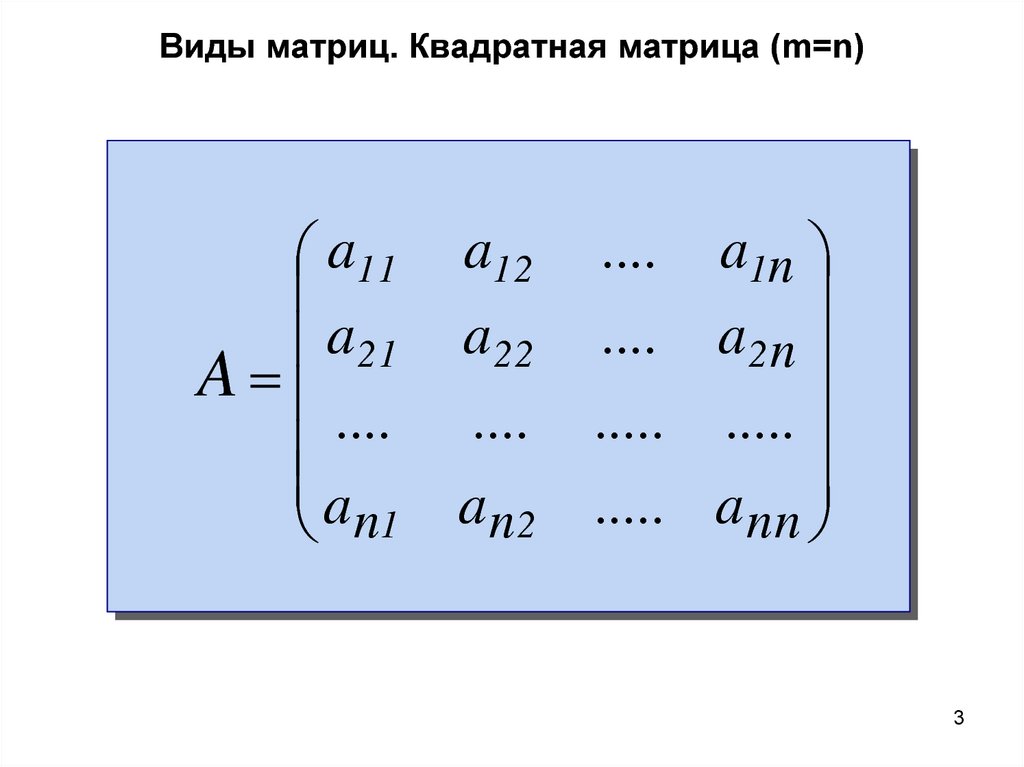
Проверьте, что матрицы, с которыми вы работаете, действительно диагональны, чтобы избежать ошибок в расчетах и алгоритмах.

Top 10 Best Xiaomi smartphones of 2024 - Ranking Xiaomi phones from budget to flagships
Для сложных вычислений с матрицами используйте специализированное программное обеспечение, которое оптимизирует работу с квадратными и диагональными матрицами.

1. Матрицы ( основные понятия, виды матриц )


Использование диагонализации матриц может значительно упростить решение задач, связанных с собственными значениями и собственными векторами.
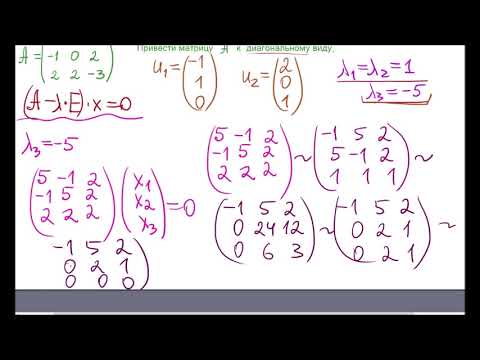
Диагональный вид матрицы. Приведение матрицы к диагональному виду. Собственные векторы
Заботьтесь о корректности ввода матриц в программное обеспечение и проверяйте их свойства перед началом вычислений.
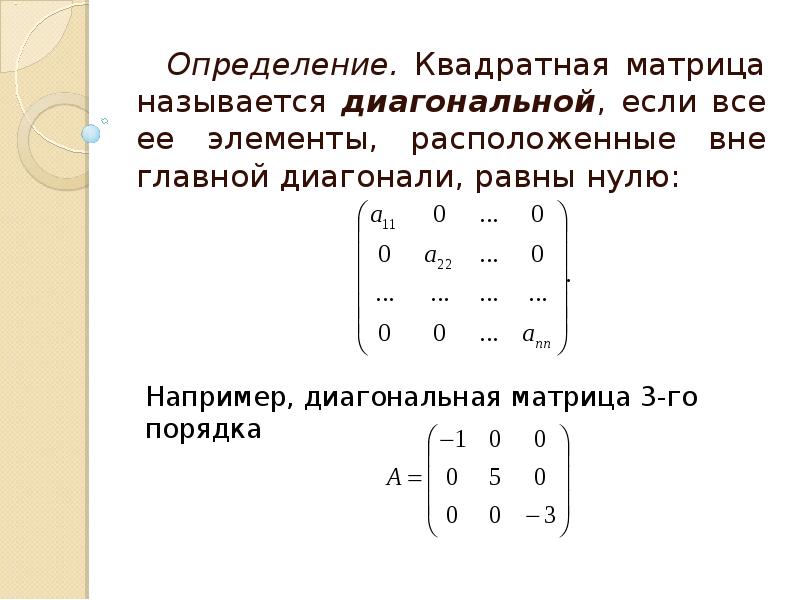
Осваивайте различные методы и алгоритмы работы с матрицами, такие как LU-разложение, для повышения своей эффективности в решении задач.


Регулярно практикуйтесь в решении задач с матрицами, чтобы улучшить свои навыки и понимание их свойств.

Обратите внимание на применение матриц в реальных задачах, таких как графика, экономика и физика, чтобы лучше понять их полезность и разнообразие.

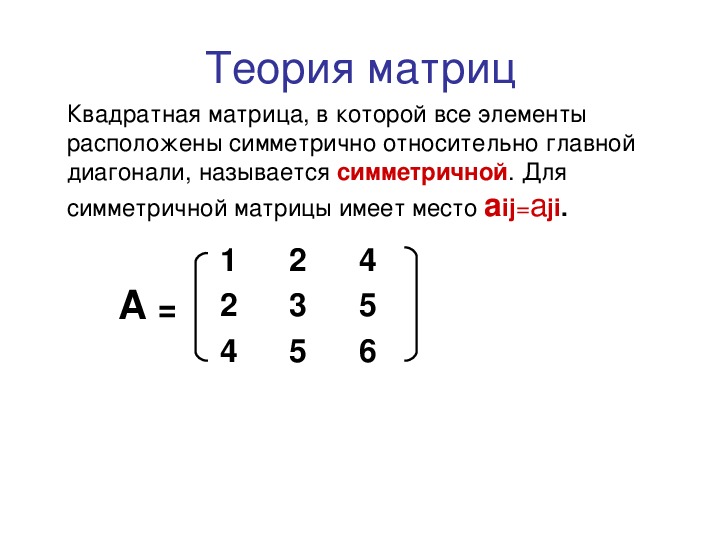

Виды матриц: транспонированная, диагональная, скалярная, ступенчатая, обратная, вырожденная