Все о медианах треугольника и их точке пересечения
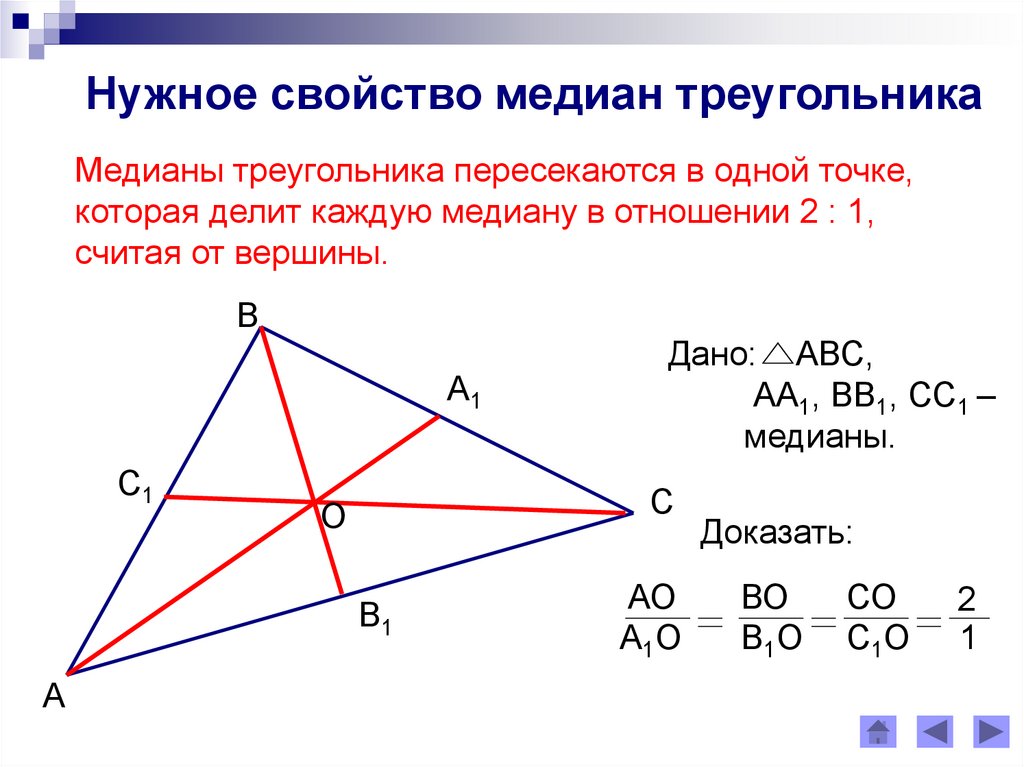
Медианы треугольника — это отрезки, соединяющие вершины треугольника с серединами противоположных сторон. Точка пересечения медиан называется центроидом и обладает интересными свойствами, которые делают её важным элементом в геометрии.


Начните с определения медиан треугольника, проведя отрезки от каждой вершины к середине противоположной стороны.
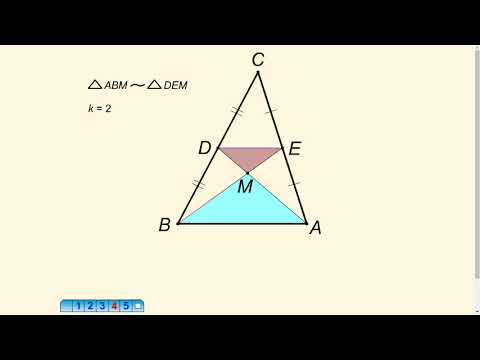
Точка пересечения медиан
Используйте линейку и циркуль для более точного построения медиан треугольника.

Точка пересечения медиан.
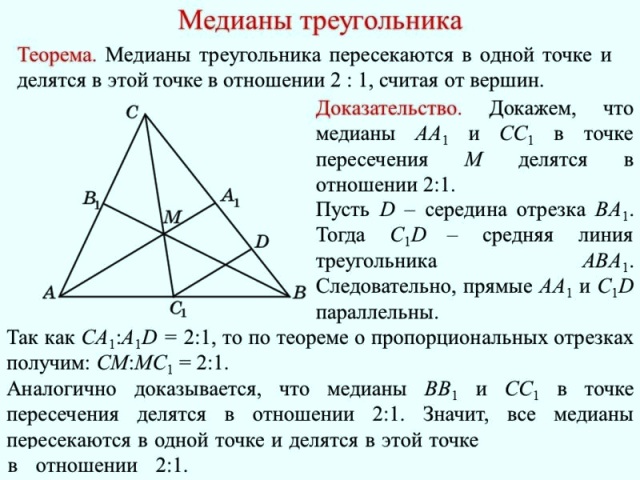
Помните, что медианы пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, начиная от вершины.

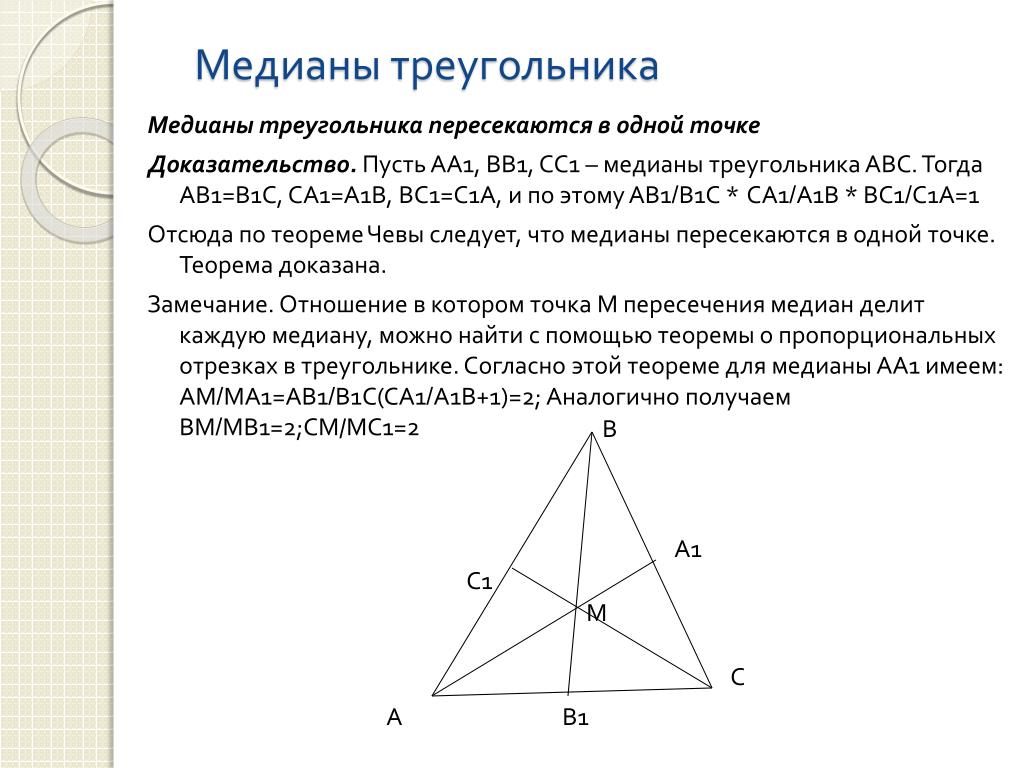
Теорема о точке пересечения медиан треугольника. Доказательство. 8 класс.
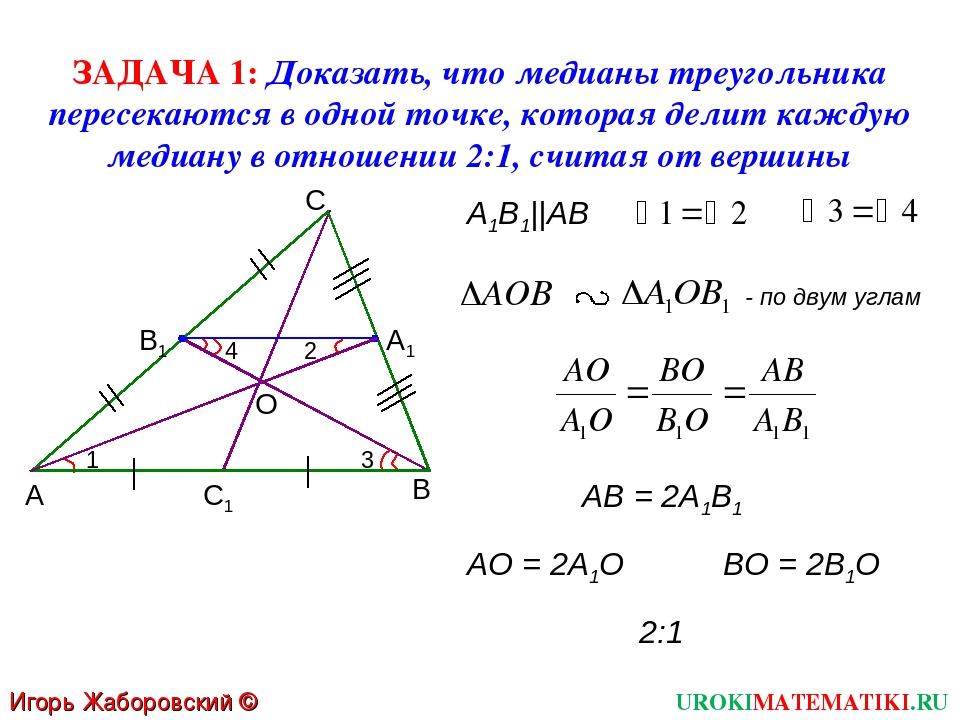
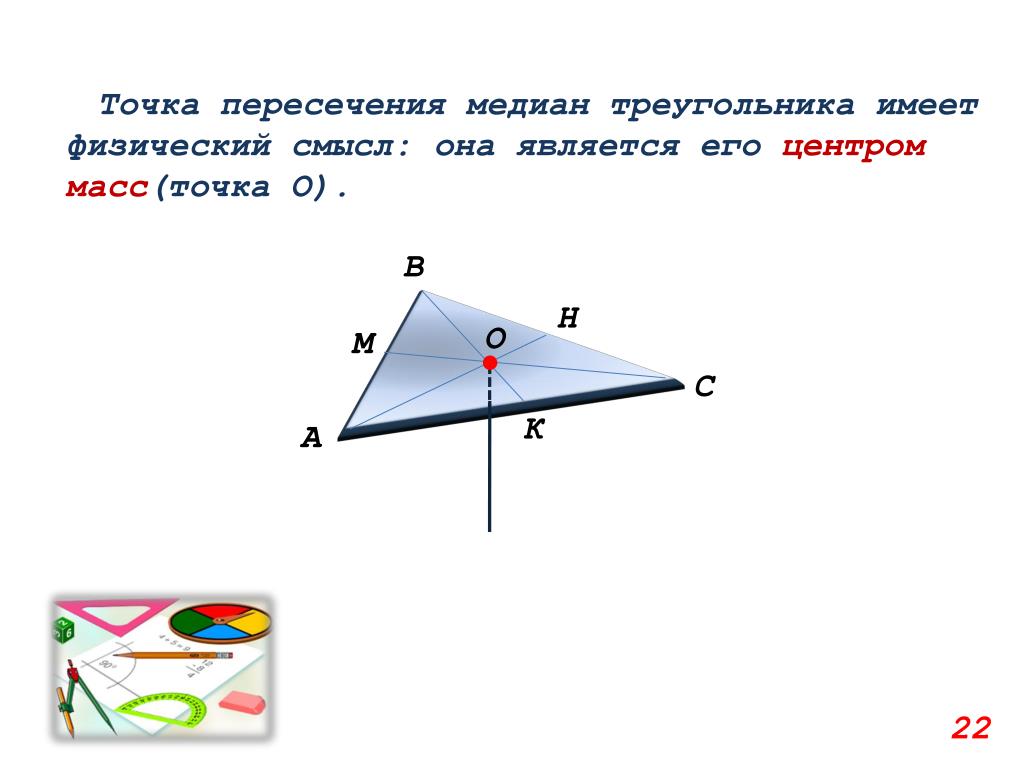
Центроид треугольника является точкой равновесия, что можно продемонстрировать, балансируя треугольник на кончике пальца в этой точке.
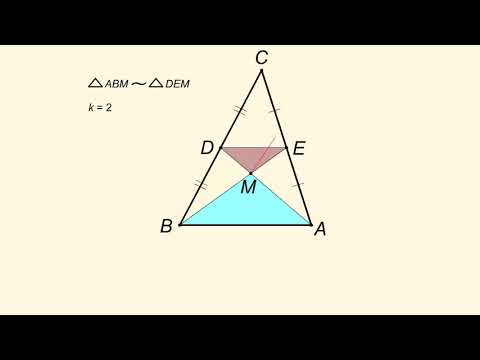
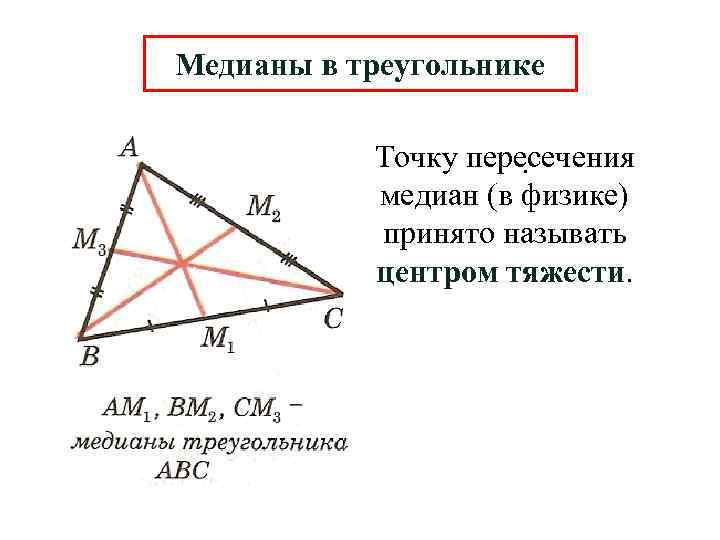
Точка пересечения медиан в треугольнике
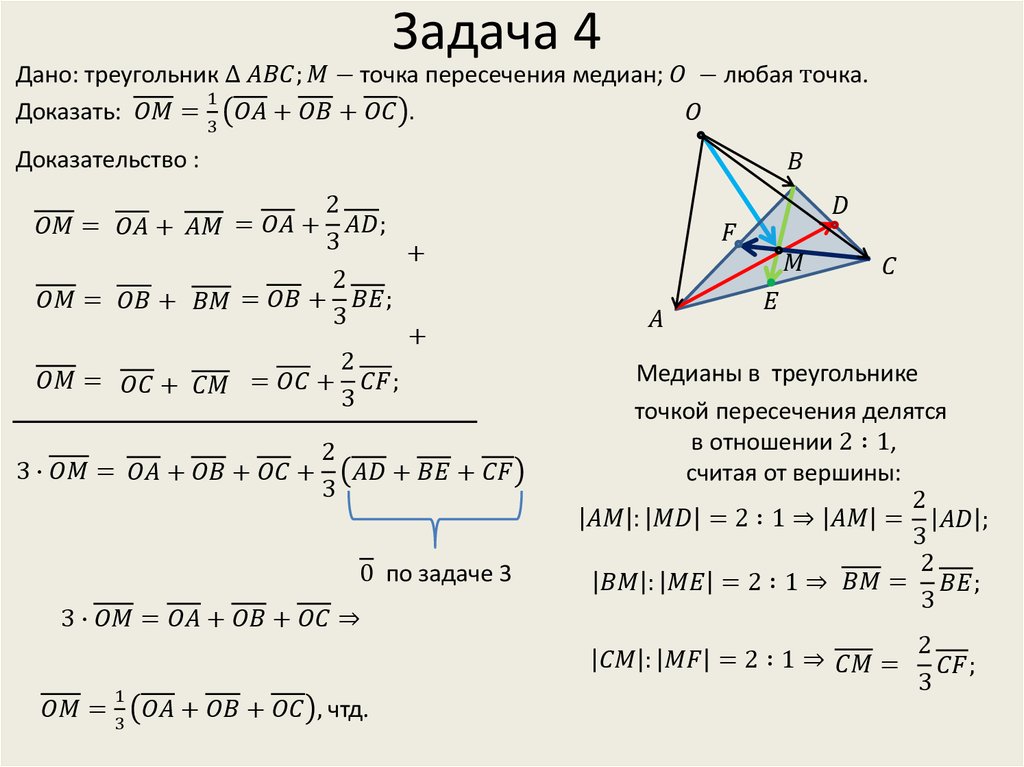
Для нахождения координат центроида, усредните координаты всех вершин треугольника.

Что даёт точка пересечения медиан в треугольнике

Медианы треугольника полезны в различных математических задачах, включая задачи на нахождение площади и центра тяжести.
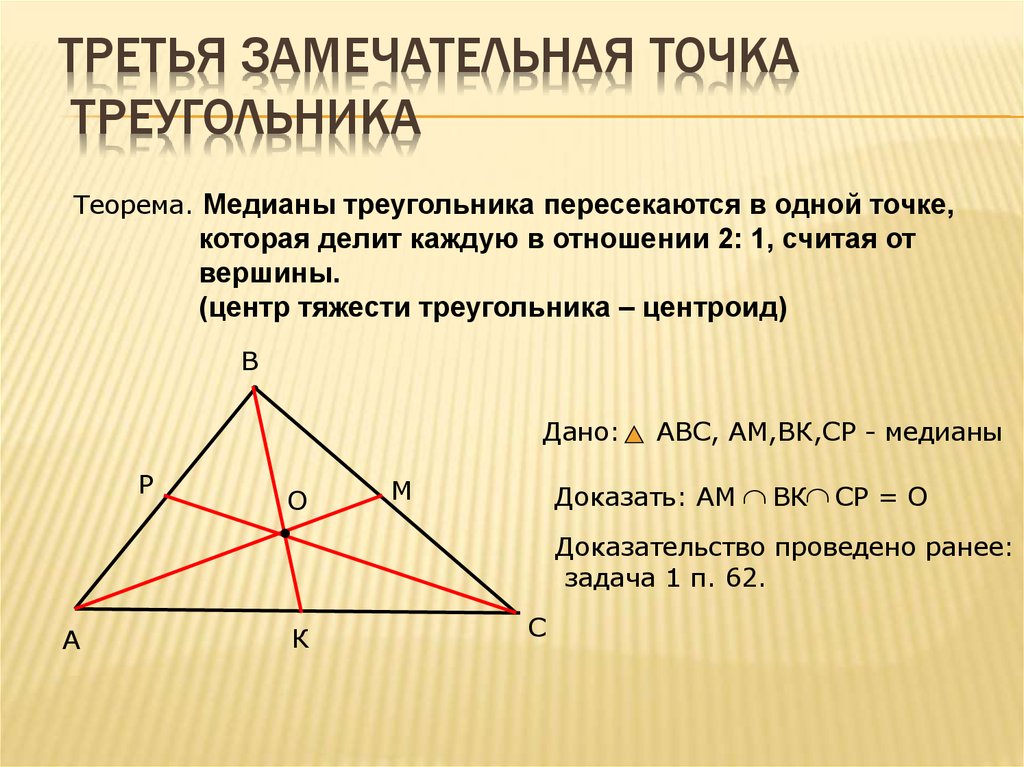

Практикуйтесь в построении медиан на разных типах треугольников, чтобы лучше понять их свойства.

Замечательные точки треугольника. Медиана треугольника.
Используйте графические инструменты или программное обеспечение для геометрических построений, если доступно.

Точка пересечения медиан треугольника.
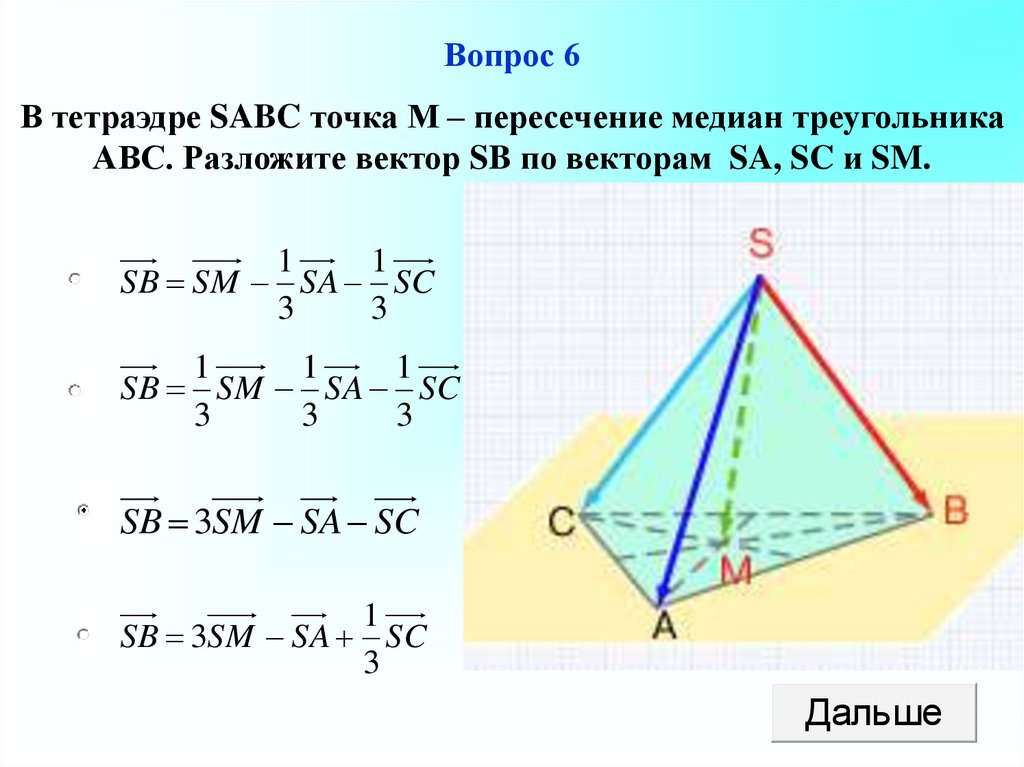
Обратите внимание на свойства треугольников, таких как равнобедренные и равносторонние, и как они влияют на медианы.

Как построить треугольник по двум сторонам и медиане, проведенной к одной из этих сторон
Изучайте реальные примеры применения медиан и центроидов в инженерии и архитектуре для более глубокого понимания.