Как эффективно решать однородные дифференциальные уравнения третьего порядка
В этом материале мы рассмотрим, как решать однородные дифференциальные уравнения третьего порядка. Здесь вы найдете пошаговые инструкции, полезные советы и примеры для лучшего понимания этой сложной темы.


Для начала необходимо убедиться, что уравнение действительно является однородным, т.е. все его члены зависят только от неизвестной функции и её производных.

Дифференциальные уравнения, 3 урок, Однородные уравнения

Используйте метод пробного решения, чтобы получить общее решение уравнения в виде суммы частных решений.

Одно уравнение

Не забывайте про линейную независимость решений; это важный шаг в нахождении общего решения.

4. Однородные дифференциальные уравнения (часть 1)

При решении уравнений с постоянными коэффициентами полезно использовать характеристическое уравнение.
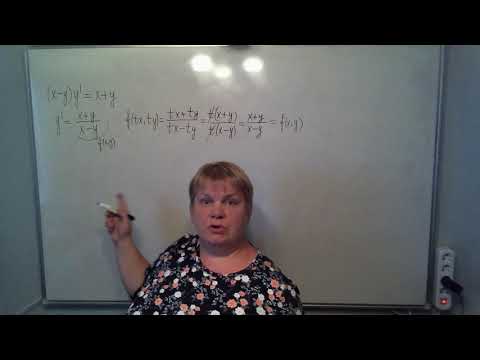
Однородные дифференциальные уравнения первого порядка

Если вы сталкиваетесь с уравнением, которое сложно решить аналитически, рассмотрите возможность применения численных методов.
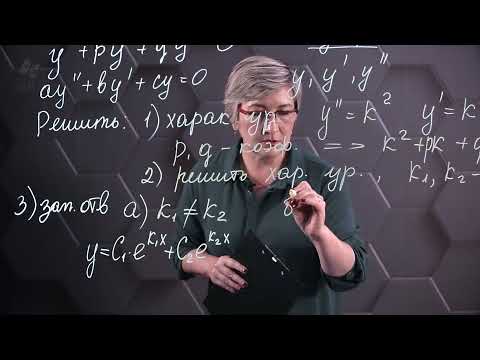
Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.


Всегда проверяйте полученные решения на их соответствие исходному уравнению путём подстановки.

Однородное линейное дифференциальное уравнение. Алгоритм решения

При работе с уравнениями, в которых фигурируют сложные функции, полезно использовать подходы, такие как метод вариации постоянных.
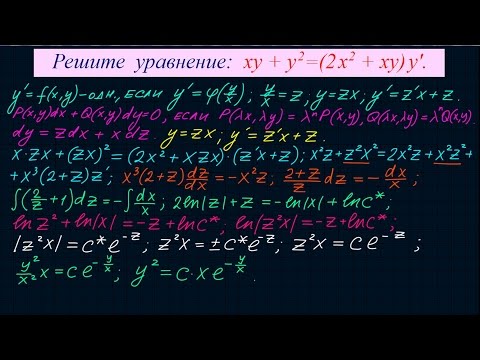
Дифференциальные уравнения #7

Используйте симметрии уравнения для упрощения процесса решения.

Однородное дифференциальное уравнение

Обращайте внимание на граничные условия, если они заданы, так как они могут существенно изменить решение.

Дифференциальные уравнения для самых маленьких


Практикуйтесь на решении разнообразных примеров, чтобы лучше понять подходы к решению однородных дифференциальных уравнений.
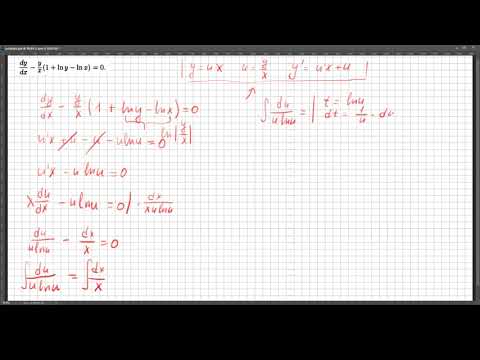
Однородные дифференциальные уравнения первого порядка#3
