Как справиться с задачами, связанными с ориентированными многообразиями

Ориентированные и ориентируемые многообразия — важная тема в математике, особенно в топологии и дифференциальной геометрии. Эта страница предлагает полезные советы и рекомендации для тех, кто изучает или работает с этими концепциями, а также собирается применить их в практике.

Понимание базовых понятий ориентированных многообразий поможет в более глубоком освоении темы. Убедитесь, что вы четко понимаете, что такое ориентация и как она влияет на свойства многообразий.

Регулярное решение задач и работа с примерами может значительно улучшить ваше понимание ориентируемых многообразий. Практика — ключ к мастерству.

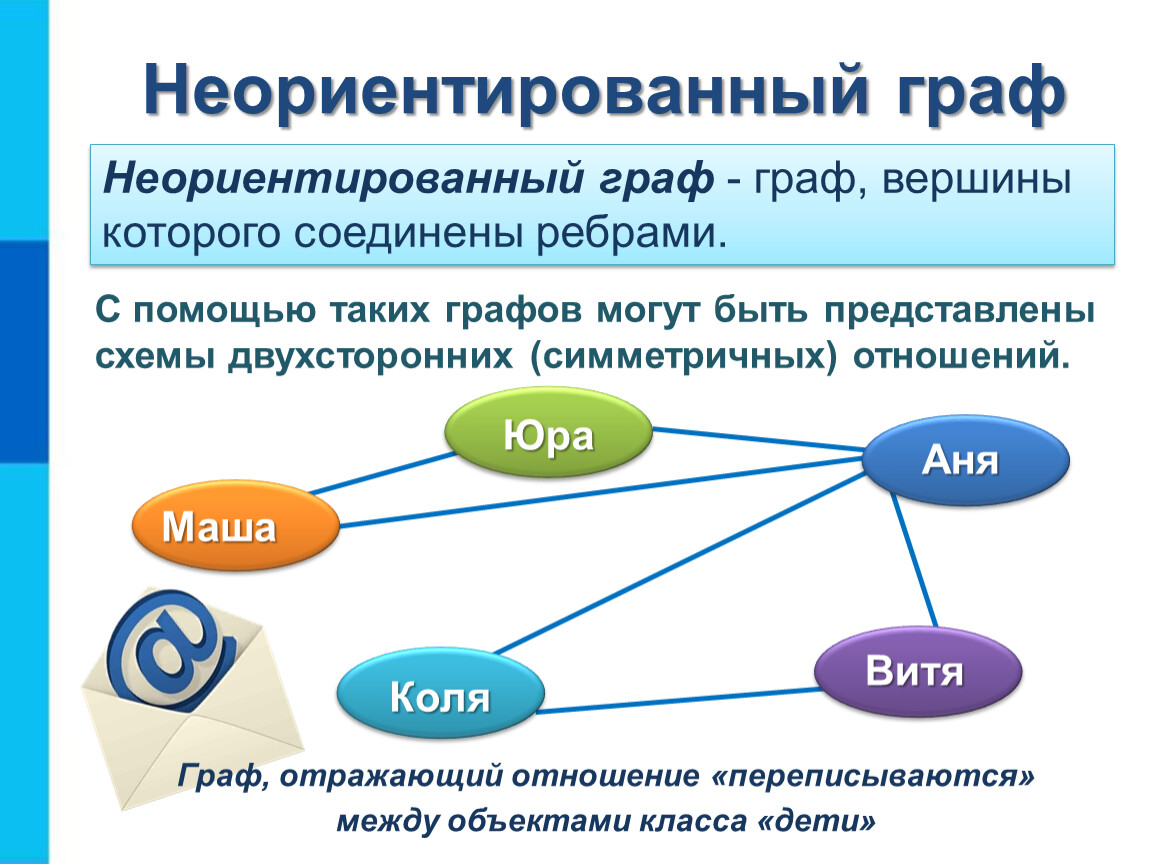
Используйте визуализации и графические представления для изучения многообразий. Они помогут лучше понять геометрические и топологические свойства объектов.

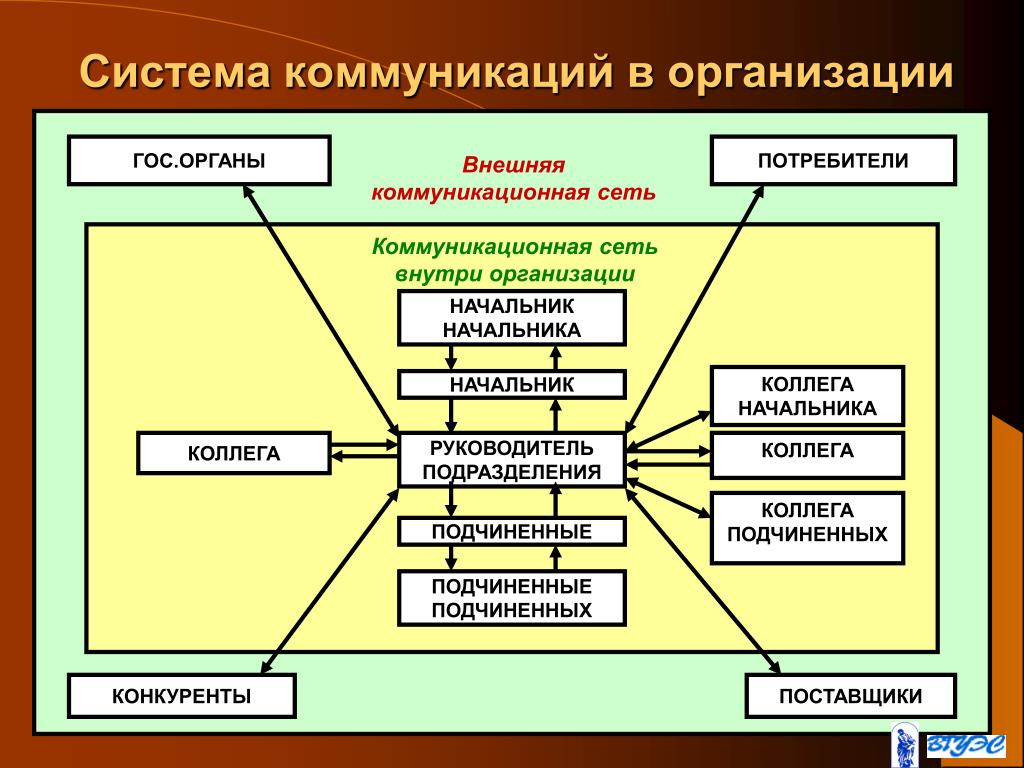
Работайте с различными примерами и задачами из реальных приложений. Это поможет вам увидеть, как теоретические концепции применяются на практике.

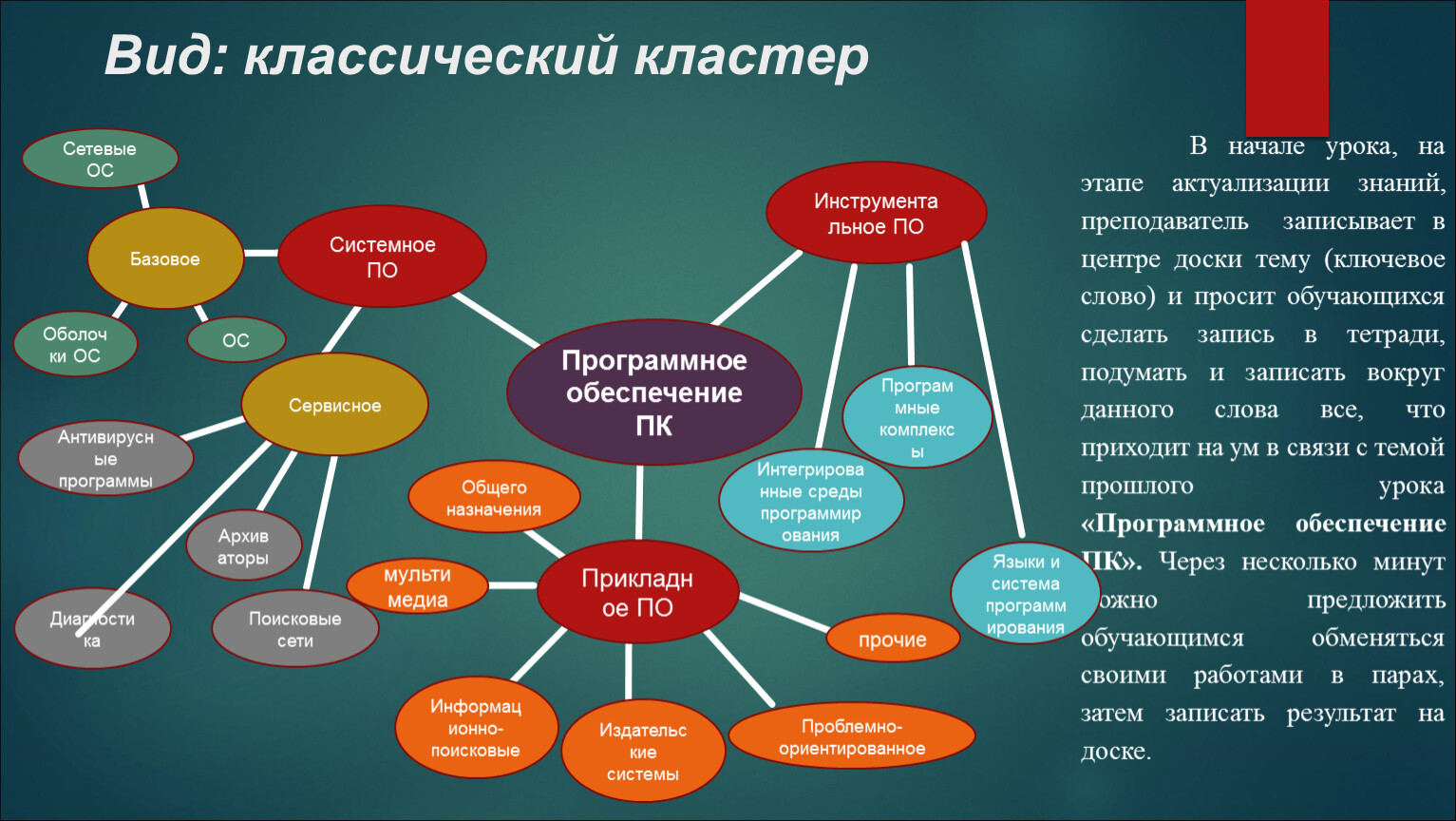
Пройдите онлайн-курсы или посмотрите видеолекции, чтобы углубить свои знания и получить новые перспективы по теме.

Читайте научные статьи и исследования по вашей теме, чтобы быть в курсе последних достижений и методов в области многообразий.

Обсуждайте сложные вопросы с коллегами или на форумах, посвященных математике. Это поможет вам лучше разобраться в трудных моментах.

Не забывайте о важности обратной связи и критического анализа своей работы. Постоянно оценивайте свои методы и подходы.

Используйте специализированное программное обеспечение для моделирования и анализа многообразий, чтобы облегчить процесс изучения и визуализации.

При необходимости обратитесь за помощью к преподавателям или наставникам, чтобы получить дополнительные разъяснения и советы по сложным вопросам.