Скалярное произведение векторов: объяснение и примеры
Скалярное произведение векторов - это фундаментальная концепция векторной алгебры, важная для понимания различных математических и физических задач. В этой статье мы подробно рассмотрим, как вычислять скалярное произведение, и предоставим полезные советы и примеры для лучшего понимания.

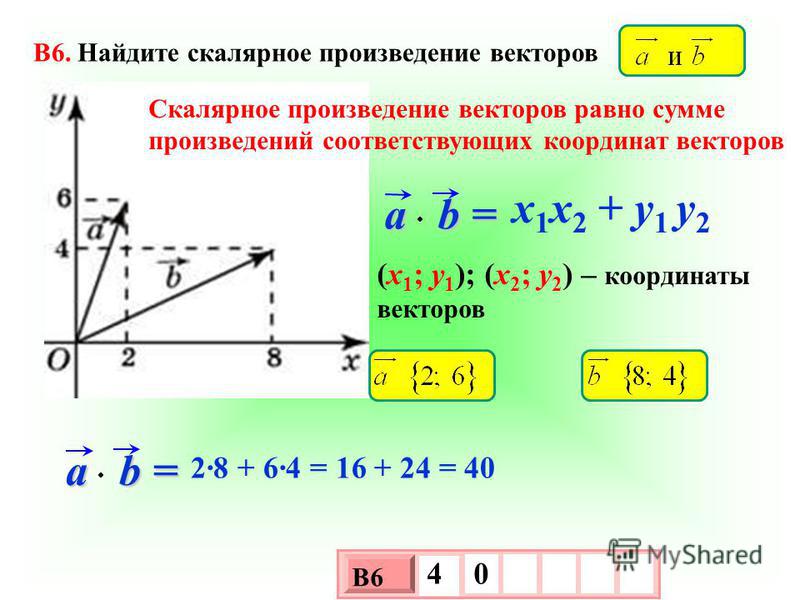

Начните с понимания базовых понятий векторной алгебры, таких как векторы, их длина и направление.

Скалярное произведение векторов. Урок 3. Геометрия 11 класс

Изучите формулу скалярного произведения: для векторов a и b это произведение их длин и косинуса угла между ними.

Лекция 18. Скалярное произведение векторов и его свойства.
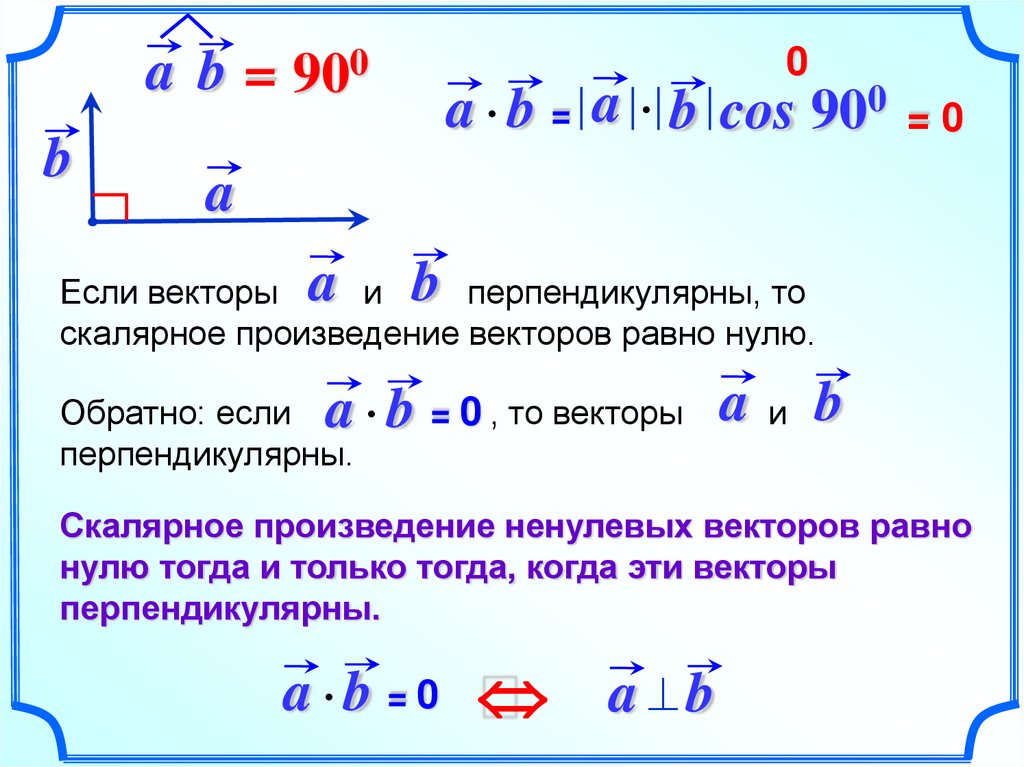
Помните, что скалярное произведение двух векторов - это число, а не вектор.

Скалярное произведение векторов. Практическая часть. 9 класс.
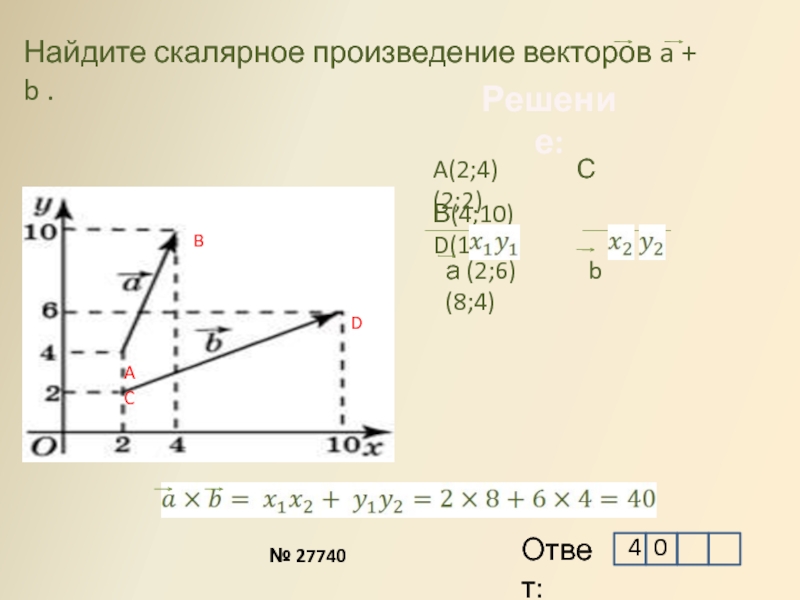
Практикуйтесь на простых примерах с известными значениями, чтобы лучше понять процесс вычисления.

Как найти косинус угла между векторами: задание 2, ЕГЭ профильная математика


Используйте графическое представление векторов для лучшего визуального понимания их взаимодействия.
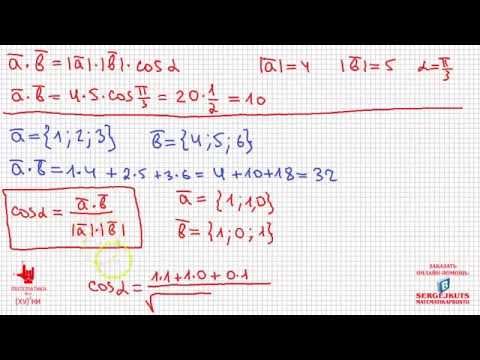
18+ Математика без Ху%!ни. Скалярное произведение векторов. Угол между векторами.
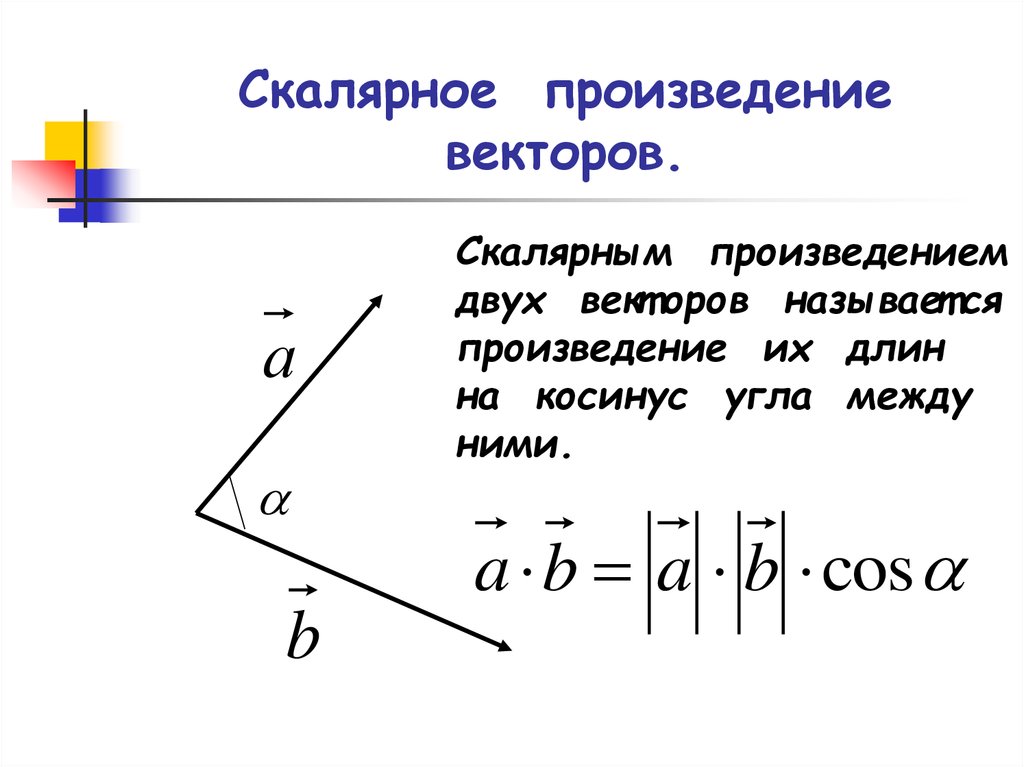
Понимание тригонометрических функций, особенно косинуса, важно для вычисления скалярного произведения.
Рассмотрите применение скалярного произведения в физике, например, при вычислении работы силы.

Скалярное произведение векторов. 9 класс.

Помните, что скалярное произведение может быть положительным, отрицательным или нулевым, в зависимости от угла между векторами.

Скалярные произведения и дуальность - Сущность Линейной Алгебры, глава 7

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика - TutorOnline
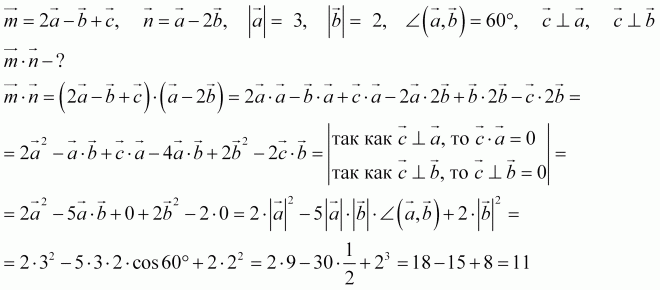
Используйте программное обеспечение для вычислений, такое как MATLAB или Python, для более сложных задач.
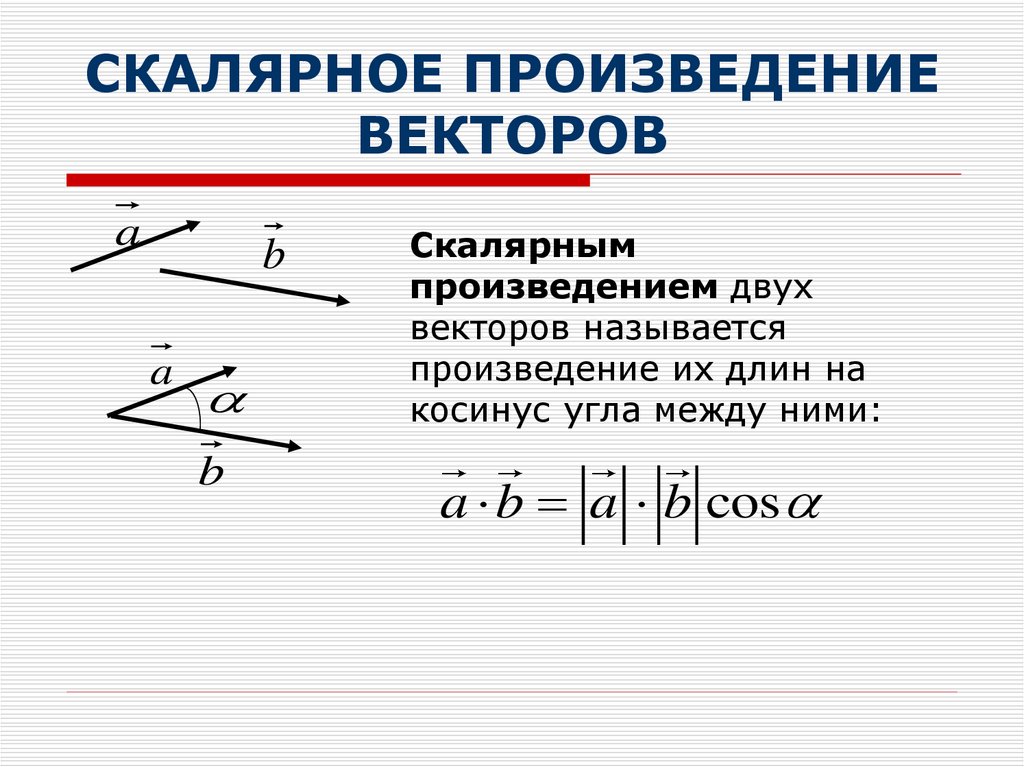

Изучите свойства скалярного произведения, такие как дистрибутивность и коммутативность, для углубленного понимания темы.
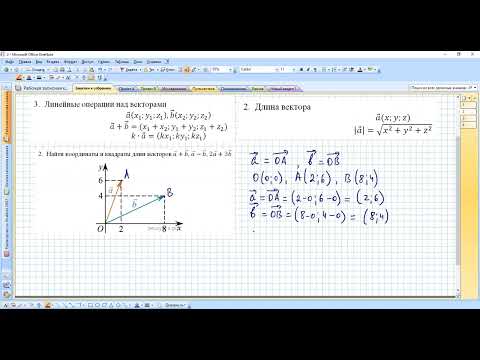
Координаты вектора. Длина вектора. Линейные операции над векторами. Скалярное произведение векторов


Скалярное и векторное произведение векторов. Линейная алгебра. Лекция 3