Эйлеров путь: полное руководство для начинающих

Эйлеров путь — это путь в графе, который проходит по каждому ребру ровно один раз. На этой странице вы найдете подборку фотографий и полезные советы, которые помогут вам понять и найти Эйлеров путь в различных типах графов.

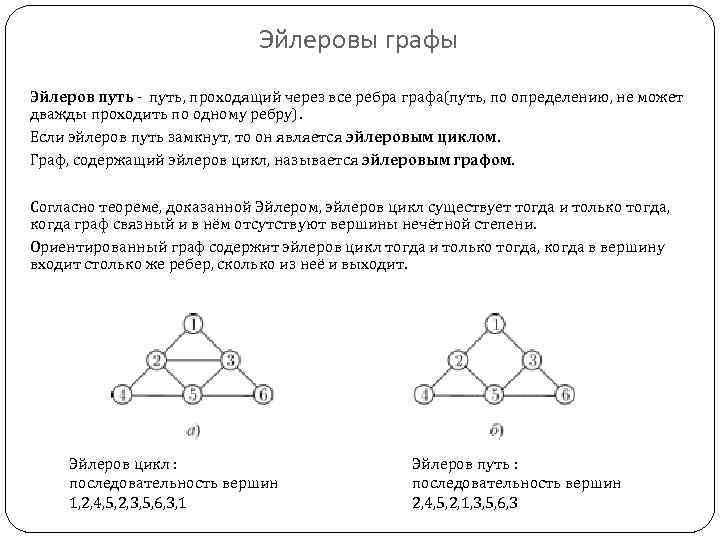
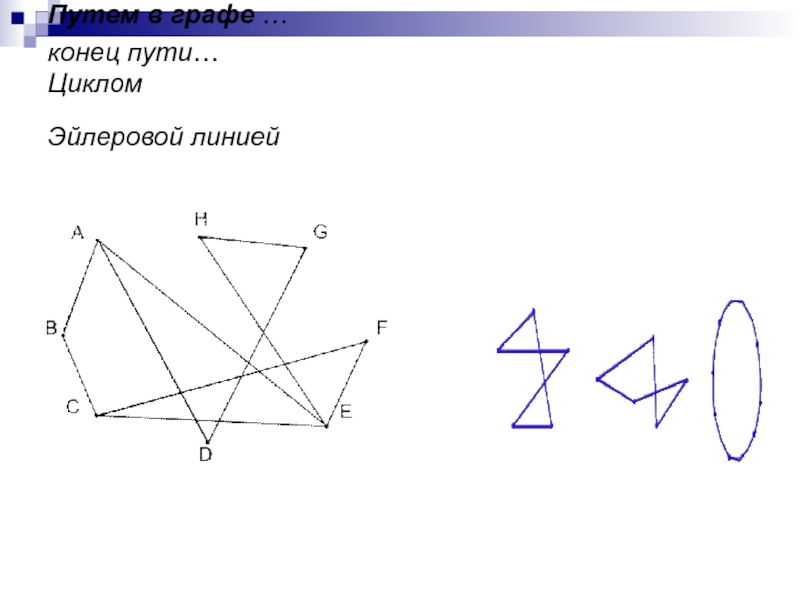
Проверьте все вершины графа на наличие четной степени. Это необходимое условие для существования Эйлерова цикла.

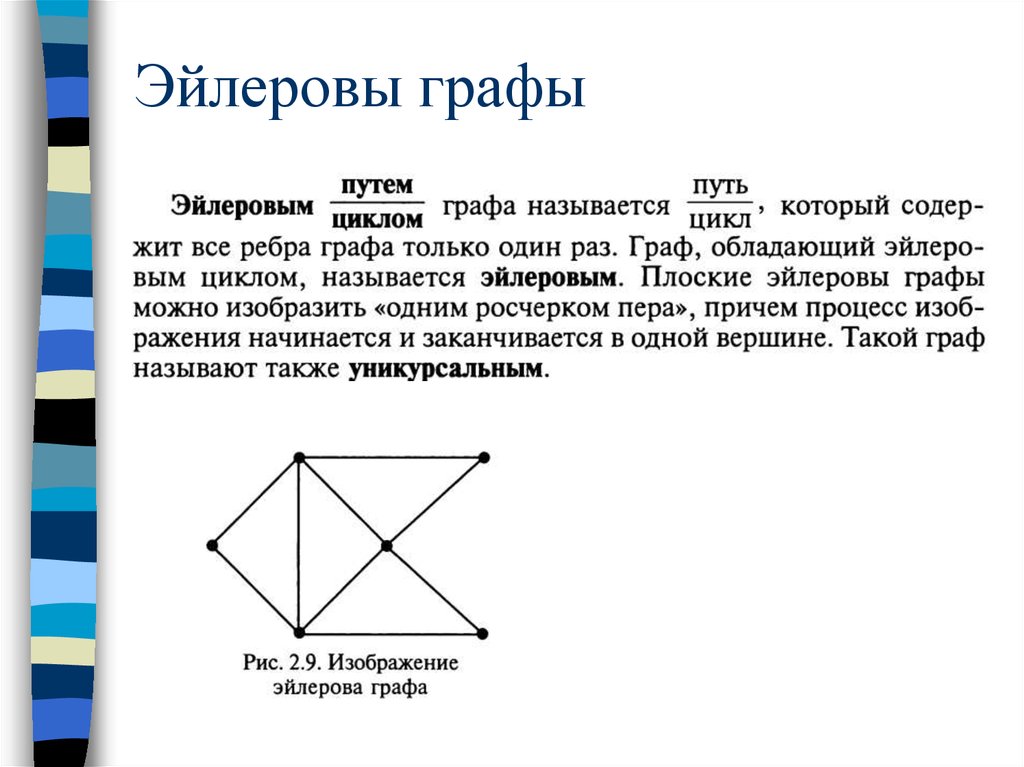
Используйте алгоритм Флёри для пошагового нахождения Эйлерова пути. Он поможет вам последовательно проходить все ребра графа.

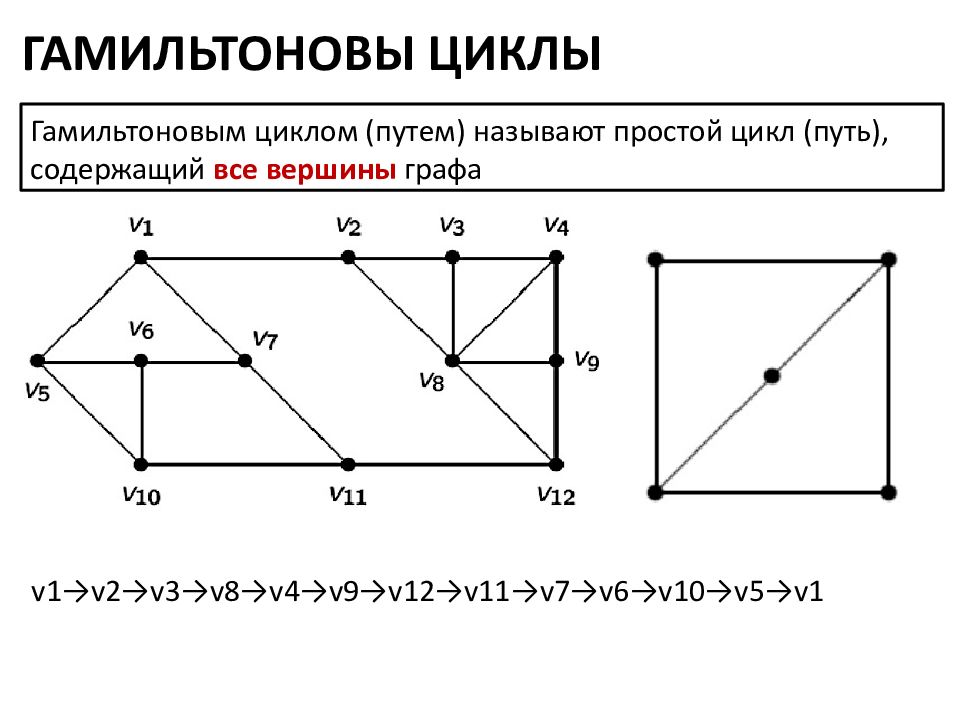
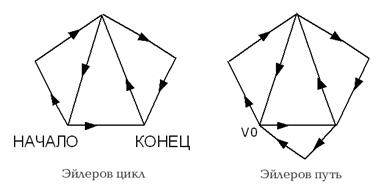
Начните с вершины, которая имеет нечетную степень, если таких вершин две. Это обеспечит правильное начало пути.

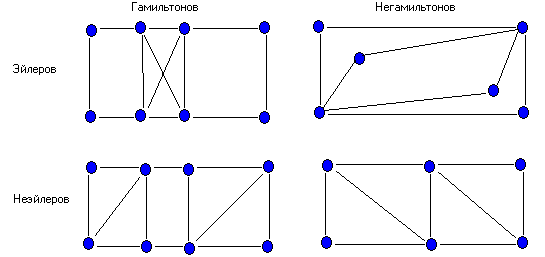
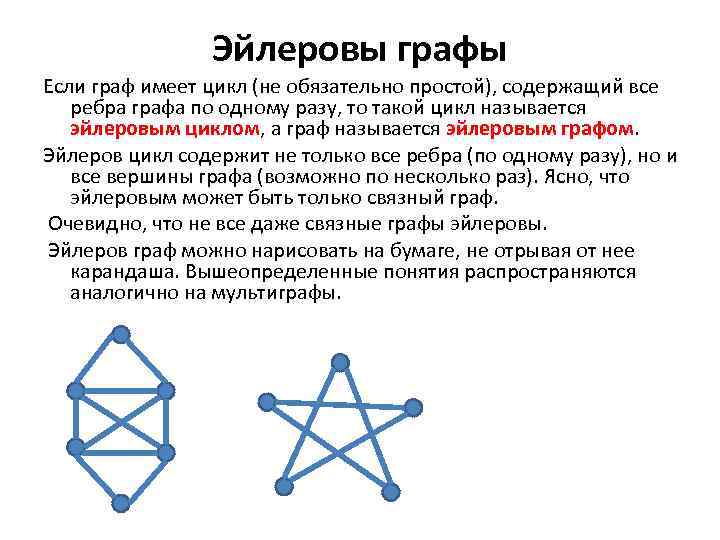
Записывайте уже пройденные ребра, чтобы избежать их повторного использования. Это поможет сохранить структуру Эйлерова пути.

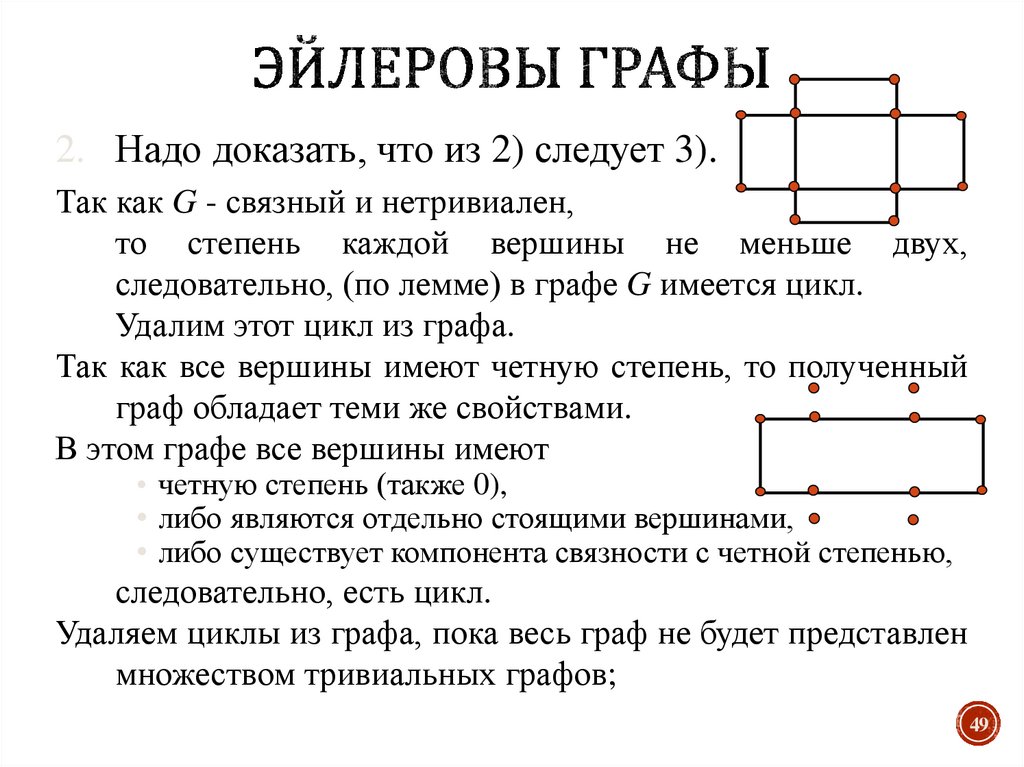
Если все вершины имеют четную степень, вы можете начать с любой вершины. Это упрощает поиск пути.

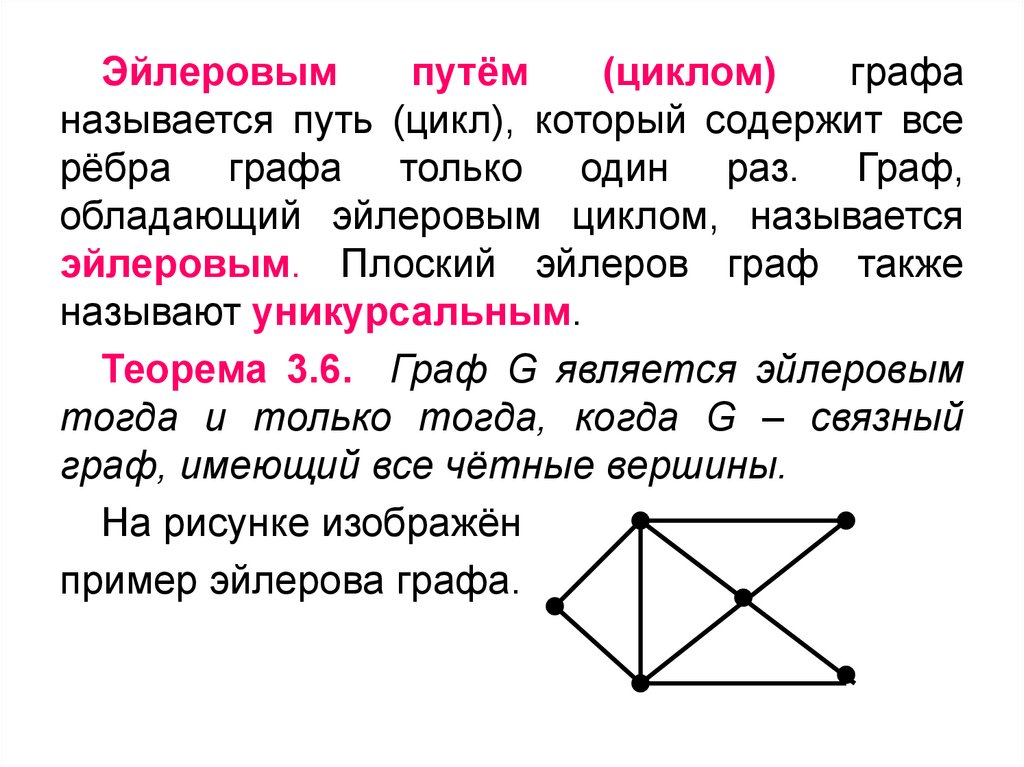
Построение мостов в графе поможет выявить критические ребра, которые нельзя удалить. Это важно для нахождения пути.

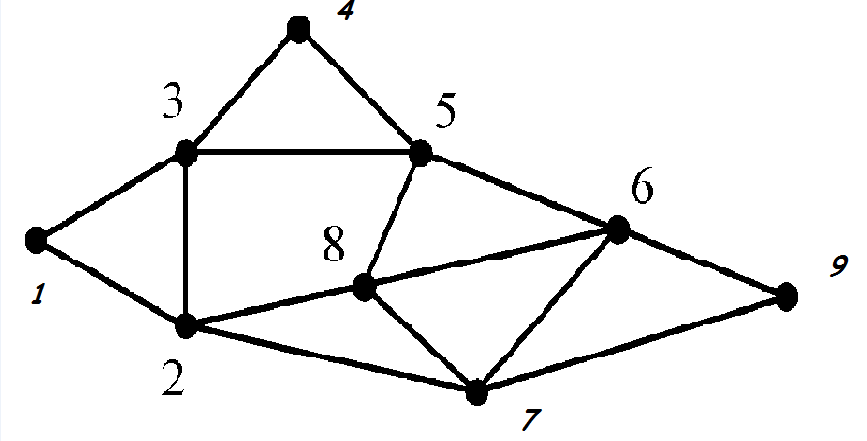
Используйте визуальные инструменты, такие как графические редакторы, для лучшего понимания структуры графа.

Применяйте алгоритм Гамильтона для проверки корректности найденного пути. Это дополнительный способ проверки.

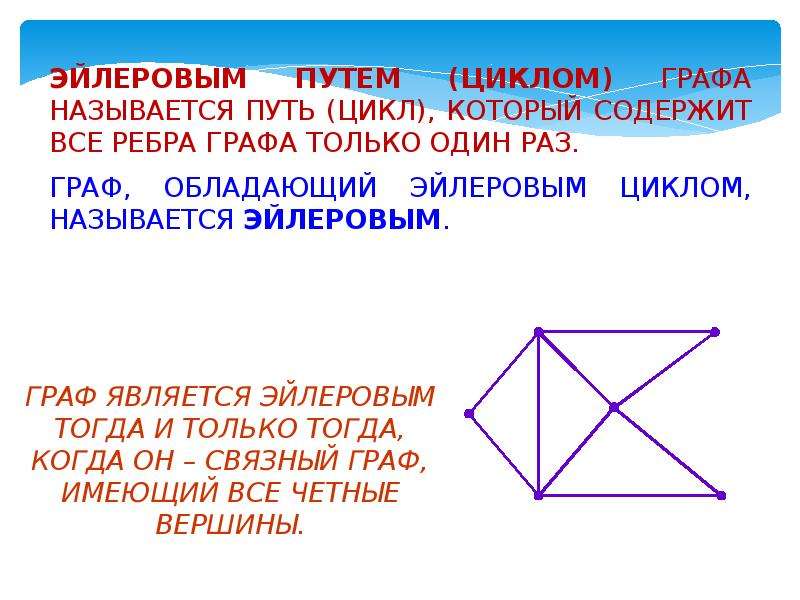
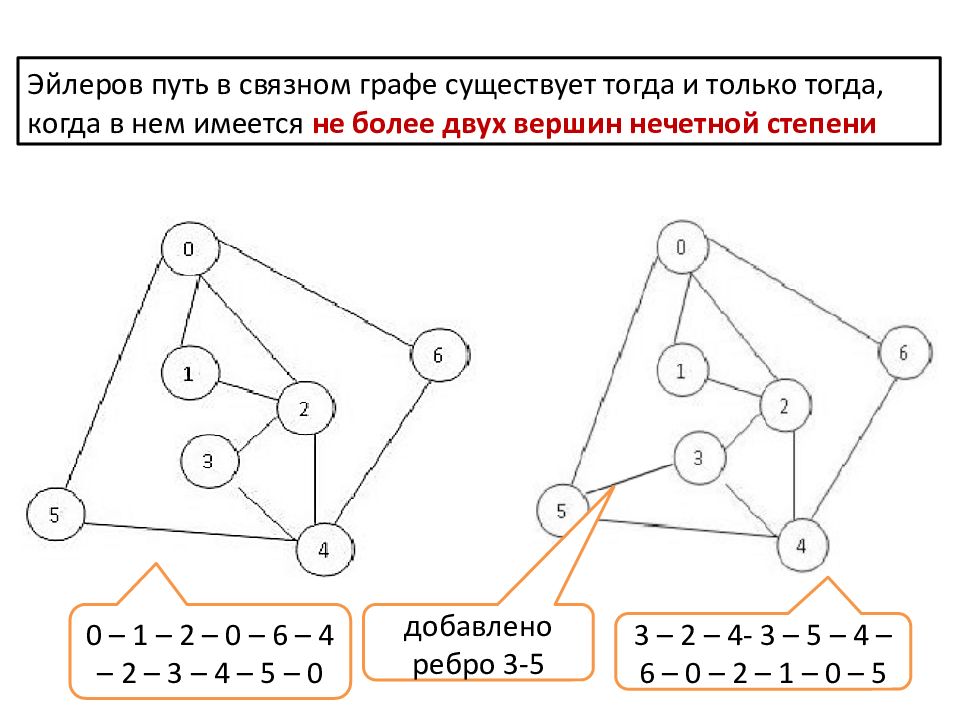
Обратите внимание на симметрию графа. Симметричные графы часто имеют более простые Эйлеровы пути.

Практикуйтесь на небольших графах перед тем, как переходить к сложным. Это поможет лучше понять основные принципы.