Изучаем формулу Эйлера для многогранников: советы и примеры для школьников
Формула Эйлера для многогранников - это важное математическое утверждение, которое помогает понять взаимосвязь между вершинами, ребрами и гранями многогранников. В этом разделе вы найдете фотографии, пояснения и полезные советы, которые помогут вам легко усвоить эту тему.

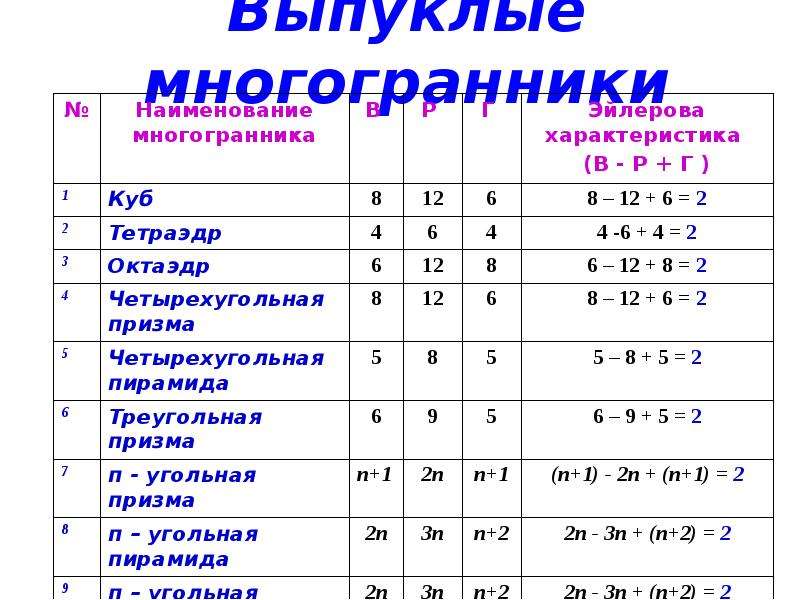
Начните с изучения основных понятий: что такое вершина, ребро и грань многогранника.

06. Формула Эйлера
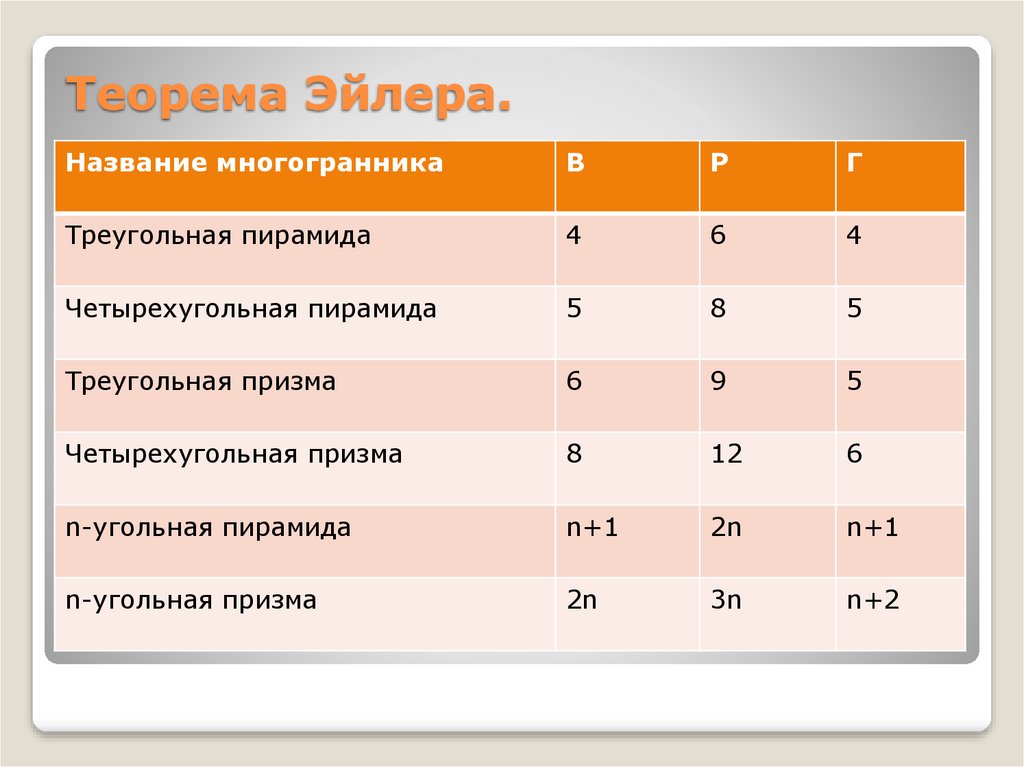
Запомните формулу Эйлера: В - Р + Г = 2, где В - количество вершин, Р - количество ребер, Г - количество граней.

#161. САМАЯ КРАСИВАЯ ФОРМУЛА В МАТЕМАТИКЕ — ФОРМУЛА ЭЙЛЕРА: e^(iπ)+1=0
Используйте наглядные примеры многогранников, таких как куб и тетраэдр, чтобы увидеть формулу в действии.

#205. Формула Эйлера для плоских графов: В-Р+Г=2 - Платоновы тела (feat. Борис Трушин)
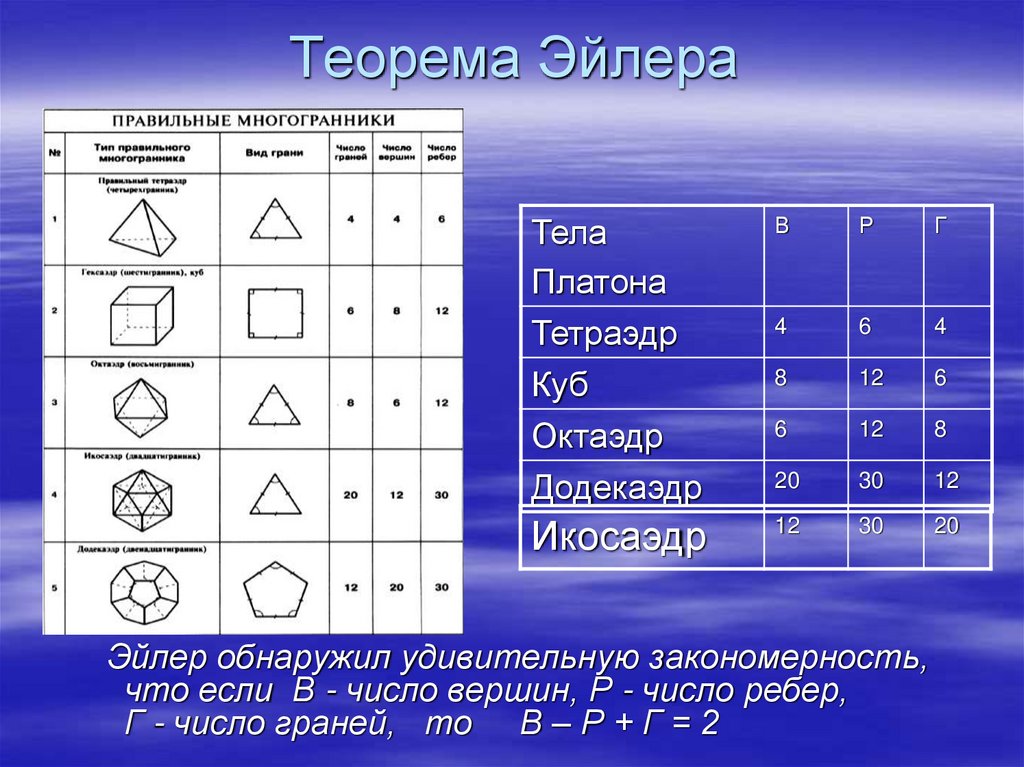
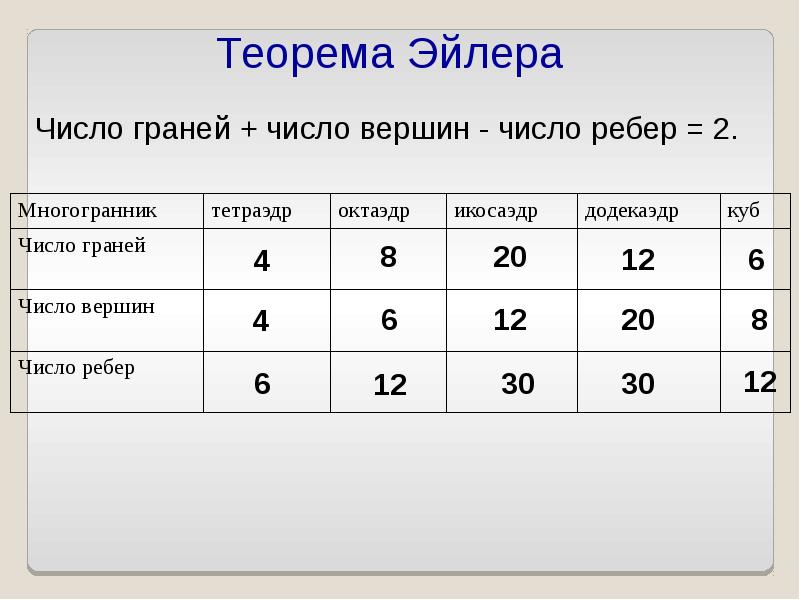
Пробуйте сами считать количество вершин, ребер и граней в различных многогранниках, чтобы лучше понять формулу.
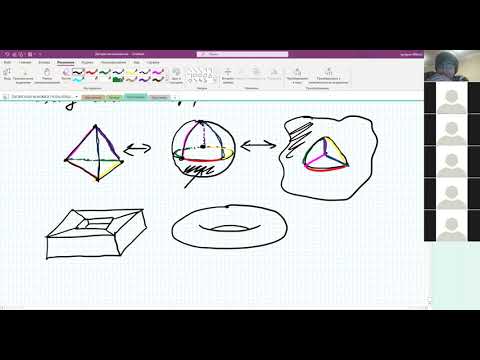
Лекция 28. Формула Эйлера и следствия из неё

Рисуйте схемы многогранников, чтобы визуализировать их структуру и облегчить понимание формулы.
ЭЙЛЕР. Грандиозное математическое наследие

Используйте программное обеспечение для моделирования многогранников, чтобы увидеть их трехмерную структуру.

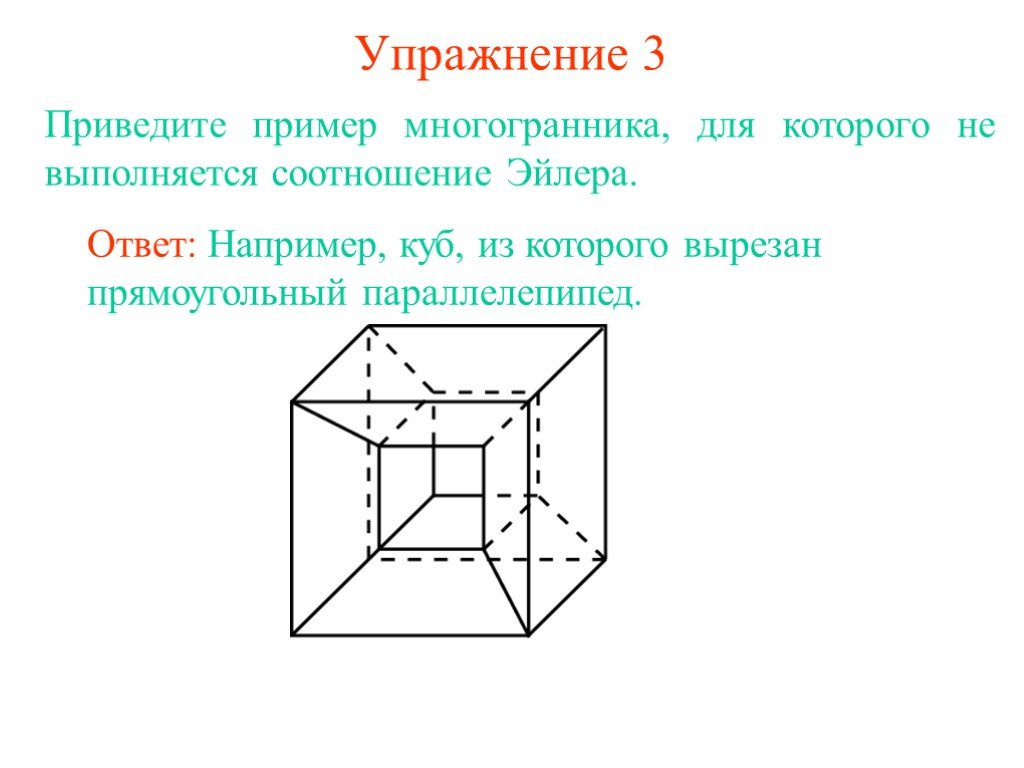
Часто проверяйте себя, решая задачи на применение формулы Эйлера для различных многогранников.

Обсуждайте задачи с одноклассниками или преподавателем, чтобы лучше понять сложные моменты.
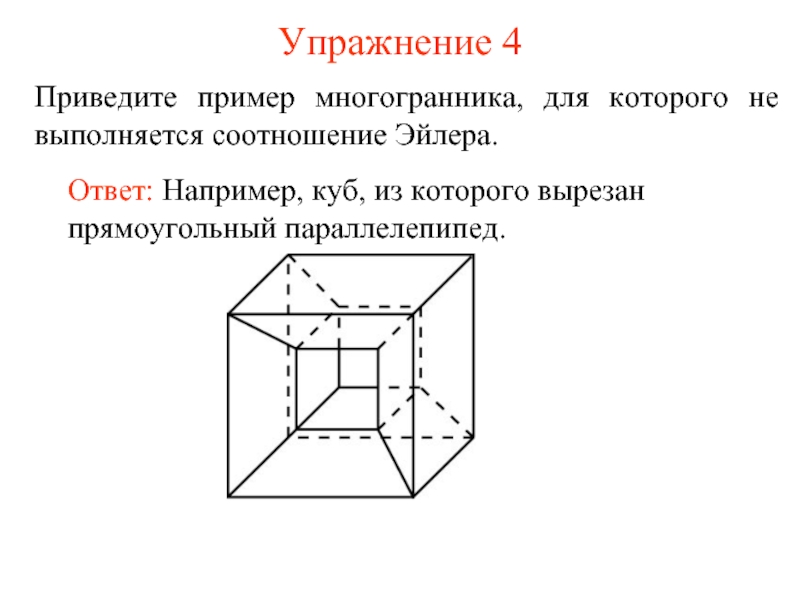
Читайте дополнительные материалы и смотрите видеоуроки для углубленного понимания темы.

Не забывайте делать перерывы и отдыхать, чтобы информация лучше усваивалась.

Формула Эйлера: объяснение - Самая красивая формула математики – Алексей Савватеев - Лекции
